例題：フィボナッチ数列

Tweet

多分、一回書いてみるのが一番早いと思います。

フィボナッチ数列とは

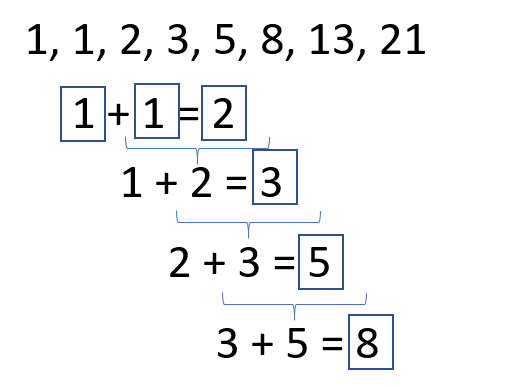
フィボナッチ数列は、「2つ前の項と1つ前の項を足し合わせていくことでできる数列」のことです。数列は「1,1」から始まり、
1, 1, 2, 3, 5, 8, 13, 21…
と続いていきます。

解いてみる

解いてみるにあたり、まず思いつくのは再帰。
ということで、再帰で検索してみた。

再帰

コード

def fib(n): if n <= 2: return 1 else: return fib(n-2) + fib(n - 1)

出力

欠点

このままでよさそうだが、
遅えぇぇぇ
40番目や100番目等後ろの値を取得するとき、処理が極端に遅くなる。
※実際、100番目を取得しようとして全然帰ってこなくて心折れた,,,

ここで出てくるのが、「動的計画法」

動的計画法

コード

# 最大値
MAX_N = 100
DP = [None] * (MAX_N + 1)  # 計算結果を保存する配列
DP[0] = 0  # 定義より
DP[1] = 1  # 定義より

def fib(n):
    # フィボナッチ数を2からnまで順に求めていく
    for i in range(2, n + 1):
        DP[i] = DP[i-1] + DP[i-2]
        print(i,'=', DP[i])
    return DP[n]

#fib()番目を出力する
print(fib(100))

出力

※100番目の出力でもすごい速い！！

動的計画法はなぜはやい？

今回に関して言うならば、余計な計算をしていないからである。

再帰の場合

同じ値を何回も求めている

動的計画法の場合

同じ値は一回だけ求めている。

2種類の動的計画法

動的計画法は、2種類存在する。
「トップダウン」と「ボトムアップ」である。

• トップダウン：メモ化再帰、メモ化
• ボトムアップ：分割統治法、漸化式ループ

※漸化式がわからない文系の諸君！！僕もです。余裕があれば別紙で解説します。
※一応画像を載せます（参考：https://juken-mikata.net/how-to/mathematics/recurrence-formula.html）

ここで抑えるべきは、「前の頁に従う」って点だと思う。

トップダウンについて

トップダウンは、計算した結果を記録して、同じ数に関しては１度しか計算しないようにする方法である。
上で紹介したコードが該当する。
下記にも一度載せる。

コード

# 最大値
MAX_N = 100
DP = [None] * (MAX_N + 1)  # 計算結果を保存する配列
DP[0] = 0  # 定義より
DP[1] = 1  # 定義より

def fib(n):
    # フィボナッチ数を2からnまで順に求めていく
    for i in range(2, n + 1):
        DP[i] = DP[i-1] + DP[i-2]
        print(i,'=', DP[i])
    return DP[n]

#fib()番目を出力する
print(fib(100))

ボトムアップ

def fib3(n):
# 0ならば、0を返す
  if n==0:
    return 0
  else:
     #fib1,2,3を定義。それぞれ、1
    fib1 = fib2 = fib3 = 1

    i = 0
    while  i < n-2:
            #それぞれ足していく
        fib3 = fib2 + fib1
        fib1 = fib2
        fib2 =fib3
        i += 1
    print(fib2)
    return fib2

...正直よくわからないなぁ,,,
理屈はわかるけど、だから？ってなりそう。

一回まとめよう

1. 動的計画法を用いると、計算量を減らせる
2. 動的計画法には二種類ある。「トップダウン」と「ボトムアップ」である
3. トップダウンは同じ計算を繰り返さないことを目的としている
4. ボトムアップは最大の値を決めておいて、実行する。

以上！