例題：コイン問題

Tweet

参考：https://o-treetree.hatenablog.com/entry/DPL1A

問題の出し方

例題

6種類のコインで15を表すとき、枚数を最も少なくする組み合わせはどれ？

額面が大きい順にコインを使うと[ 12, 1, 2]の三種類になる。
しかし、答えは[ 7 , 8 ]の二種類になる。
じゃあ、どんな計算をすれば、答えが出るの？ってのを解説します。

解き方

イメージ編

DPテーブルを作成する

動的計画法の定義にあるように、"問題を複数の部分問題に分割して、部分問題の計算結果を利用して元の問題を解く"を実行するために、計算結果を格納するテーブルを作成する。
DPテーブルは、数値を表現するために、枚数が最も少なくなる組み合わせを記録している。

実際にテーブルを作ってみると、こんな感じになる。

• I：使えるコインの種類
• J：表現する値

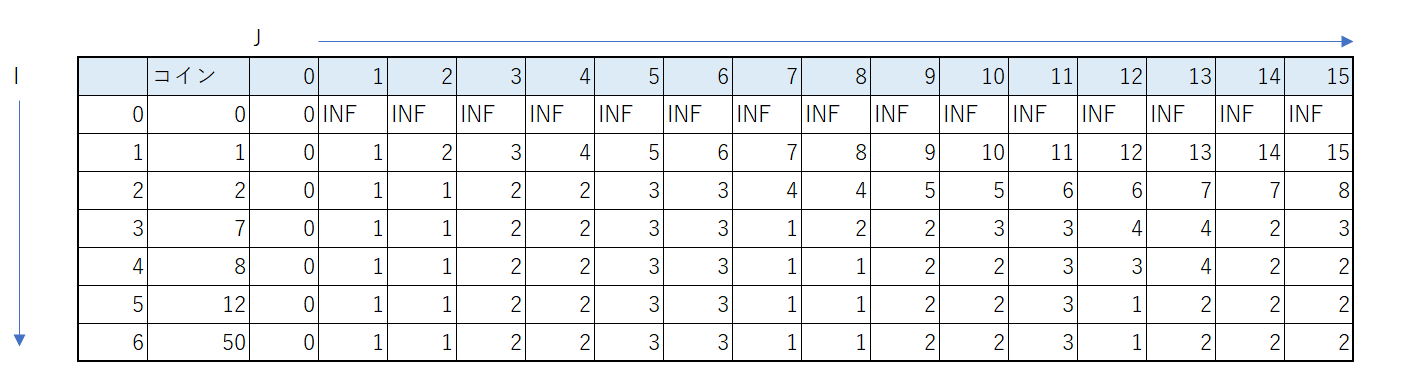
DPテーブルの見方と表現

上図(DPテーブル)は、一見とっつきにくく思えるが、見方さえ覚えれば、割と楽です。
本項では、DPテーブル見方と表現方法を例とともに記します。

例：J = 8の時

今回は、例題としてJ(表現する値)＝8の時を例に解説する。
J=8は、下図で赤く囲っている箇所である。

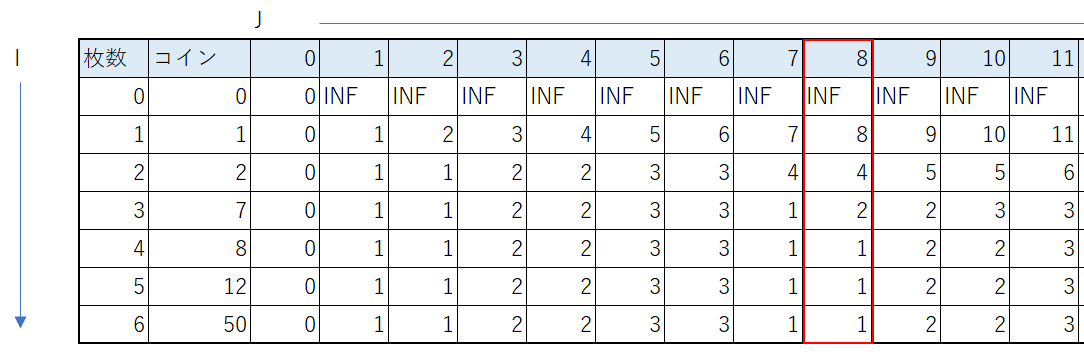
赤く囲っている箇所を見ると、「8 ・・4・・」と数値が異なる。
数値が異なっている理由は、「使えるコインの種類が増えた」からである。
つまり、下進むほど、使えるコインの種類が増え、少ない枚数のコインで値を表現できる可能性が増える。

I=0の時

使えるコインの種類：0

0枚のコインでは8を表現できないため、値はINF

I=1の時

使えるコインの種類：１(１)

8を1で表現する場合、コインが8枚必要なるため、値は8

I = 2の時

使えるコインの種類：2(1 , 2)
※8を表現するのに、1と2の二枚を使用できる

8を1 , 2で表現する場合、コインが4枚必要になるため、値は4

I = 3の時

使えるコインの種類：3(1 , 2 , 7)
※8を表現するのに、1と2と7の三枚を使用できる

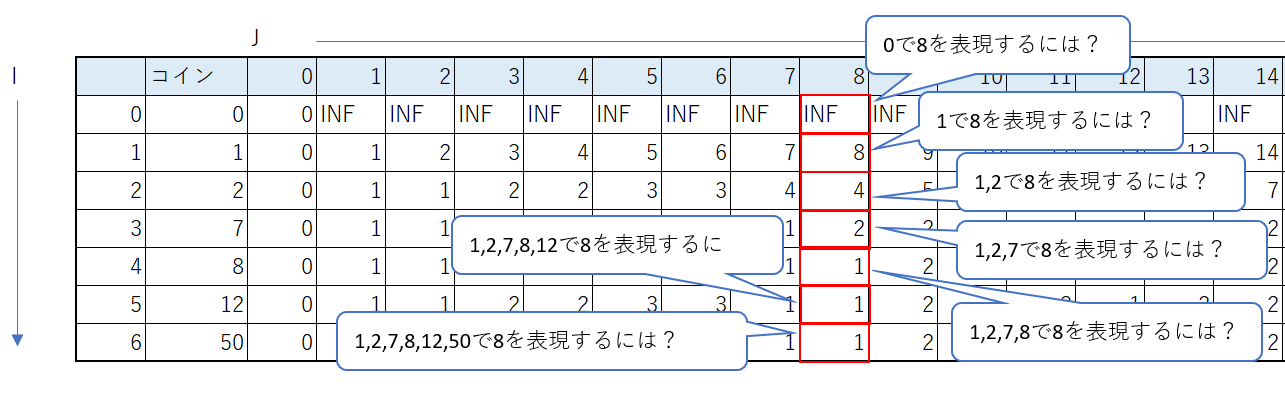
8を1 , 2 , 7で表現する場合、コインが2枚必要になるため、値は2

と、続いていく。つまり、下図のようなことをしている。

実装1

コード

かなりざっくりしている気がする。
テーブルを作る前に、ターゲットを絞って最小の組み合わせを表示するアルゴリズムを作ってみた。
※これ、厳密な意味では動的計画法ではないのでは？もう少し調査します

COINS = [1, 2, 7, 8, 12, 50]
target = 15
length = len(COINS)
cntMemo = []
#とりあえず、初期値として最多手数を入れる
#初期値の設定
if cntMemo == 0:
    cntMemo.append(0)
else:
    cntMemo.append("INF")
#コインをしまう処理
def select(type):
    num = type-1
    #現在の値
    memo = COINS[num]
    #必要な種類
    cnt = 1
    while True:
        if memo == target:
            break
        if memo >target:
            memo -= COINS[num]
            num -=1
            memo += COINS[num]
        if memo < target:
            cnt += 1
            memo += COINS[num]
    #cntの最小値をメモとして保存する処理
    if len(cntMemo) == 1:
        cntMemo.append(cnt)
    else:
        if cnt < cntMemo[type-1]:
            cntMemo.append(cnt)
        else:
            cntMemo.append(cntMemo[type-1])
    return cnt
def coin():
    cnt = target
    if cntMemo[0] == 0:
        cnt = 0
    else:
        type = 1
        while type <= length:
            select(type)
            type += 1
                     # コインの種類が最小の組み合わせが見つかったとき
        cnt = cntMemo[type-1]
    return cnt
print(target, "を表現するためには、", coin(), "種類のコインが必要")
for memo in cntMemo:
    print(memo)

出力

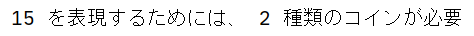
実装2

今度は、テーブルを作成していく。

実装

# コインの種類
COINS = [1, 2, 7, 8, 12, 50]
# 求める範囲(30までのテーブルを作成する)
coverage = 30
# 求める値
target = 15
dp = [[[]for j in range(coverage+1)] for i in range(len(COINS) + 1)]
def serachNum(i,j):
    target = j
    num = i - 1
    # 現在の値
    memo = COINS[num]
    cnt = 1
    while True:
        # ここの処理は変更していない。
        if memo == target:
            break
        if memo > target:
            memo -= COINS[num]
            num -= 1
            memo += COINS[num]
        if memo < target:
            cnt += 1
            memo += COINS[num]
    return cnt
def coinChange():
    for i in range(len(COINS)+1):
        for j in range(coverage + 1):
            if i == 0:
                # 0行目の時の処理
                if j == 0:
                    # 配列0個目
                    dp[i][j] = 0
                else:
                    # 配列1個目以降
                    dp[i][j] = "INF"
                print(j)
            else:
                # 1行目以降の処理
                if j == 0:
                    # 配列0個目
                    dp[i][j] = 0
                else:
                    # 配列1個目以降
                    # 一つ前のコインの組み合わせ方を取得
                    # 今回求めたコインの組み合わせを取得
                    comparison = dp[i-1][j]
                    ans = serachNum(i,j)
                    if type(comparison) == int:
                        if ans < comparison:
                            # 今回の組み合わせが最短手だった時
                            dp[i][j] = ans
                        else:
                            # 前回以前の組み合わせが最短手だった時
                            dp[i][j] = comparison
                    else:
                        # 一つ前の最短手が数字ではないとき
                        dp[i][j] = ans
def coinGet(type,target):
    return dp[type][target]
coinChange()
ans = coinGet(len(COINS),target)
print(len(COINS),"種類のコインを使って",target,"を表現するには",ans,"種類のコインが必要")

出力

お、いい感じの値が求められている。
今回のコツは、前回求めた最短手をメモしておき、今回求めた最短手と比較することだと思う。