1635 views
Sarsa
はじめに
sarsaは価値反復報酬型の強化学習アルゴリズム。
こちらの本を参考に自分が理解した内容の整理を行っていきます。
前ページと同様、次の迷路を考えます。
お題
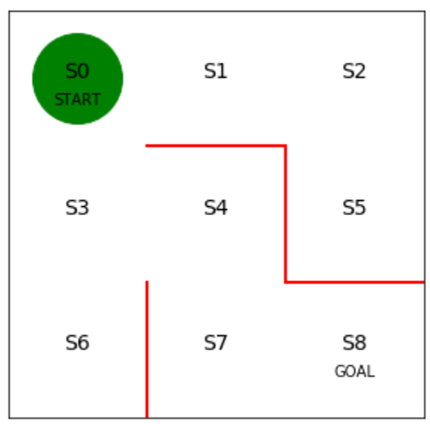
下図の迷路があり、緑色がプレイヤー、赤線は壁、S0~S8はプレイヤーの移動先である。
スタートであるS0からゴールのS8に移動したい。
プレイヤーは上下左右に移動できるが、斜め方向には移動できない。
最短経路である、S0→S3→S4->S7→S8に移動する経路をプログラムで発見するにはどうすればよいか。
Sarsaで解く
方策反復法では、方策の確率に従って経路の選択を繰り返し、ゴールに向かいました(方策反復法は前ページを参照してください)。
そして、ゴールにたどり着いたら、通った履歴から最適な方策の確率を作成していく、といった手法でした。
そのときの方策は、こんな感じでした。
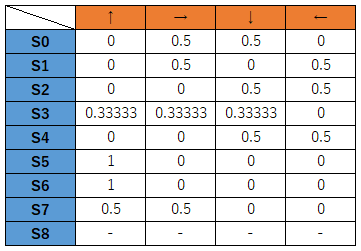
最初に均等に確率を分配し、不要な経路の確率は下がり、必要な経路の確率が上がっていくというものです。
これを図式化するとこんな感じです。
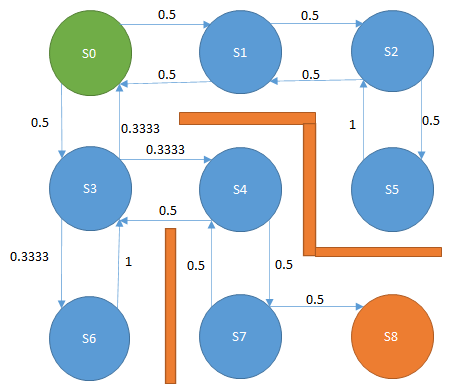
S0においては右か下に移動する確率は0.5ずつで、探索を繰り返すたびに各ノードに伸びる確率を更新していくというものです。
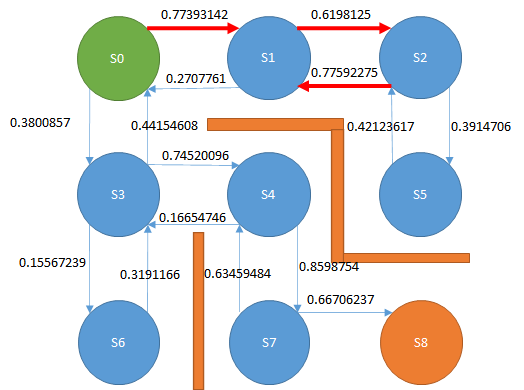
Sarsaにおいても同様ですが、この経路の確率を最初は乱数で生成します。
こんな感じ。
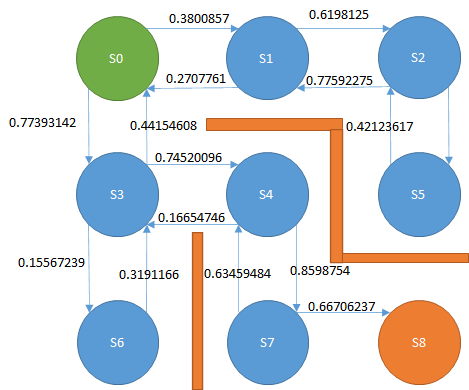
この数値のことをQ値と呼びます。
そして、エージェントは基本的に経路の値が大きいほうを選択して移動していきます。
S0の場合、右に0.3800857、下に0.77393142の数値が割り当たっています。
ですので、選択するのは下、ということになります。
ここで方策勾配法と違うのは、方策勾配法は0.3800857の確率で右に移動、0.77393142の確率で下に移動する、と考えていましたが、Sarsaでは基本的に最も大きな数字の経路を選択します。
ただし、最も大きな経路をたどっていくと、S0→S1→S2→S1→S2→S1→S2→S1→S2→S1・・・
とループしてしまい、一生ゴールに辿り着きません。
そこで、e-greedy法を使います。
e-greedy法は、時々ランダムに、経路の値を無視して別の経路を選択するというものです。
ですので、上記のようにS1とS2を行ったり来たりしていても、たまたまS1でランダムにS0に移動する経路を選択することもある、ということです。
そうすることで、探索の袋小路に陥ることを防ぎます。
そして、Sarsaでは場所を移動するたびにQ値を更新していきます。
Q値の更新式はこう書かれています。
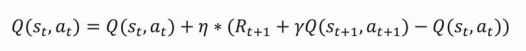
ηはイータと読みます。
イータは小さな値、γ(ガンマ)は割引報酬率です。
そして、以下の式の赤枠部分をTD誤差と言い、この値が0になるようにQ値を更新していきます。
ここがややこしい…。
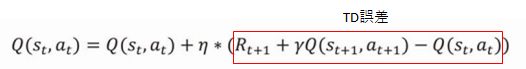
まず、この式が何を計算しているのかというと、S0地点においては赤字の部分を計算しています。
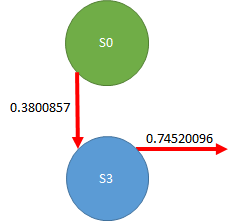
つまり、こういう計算をしています。
0.3800857 + η*(0 + γ(0.74520096 - 0.3800857))
0.3800857は下矢印のQ値です。
0は報酬です。冒頭で紹介した本では、S8に辿り着いたときだけrは1となります。
ようするにS0からS3に移動しただけではゴールしていないのでご褒美なし、というのが0の意味です。
次にγより後ろの0.74520096 - 0.3800857ですが、この意味がよくわからないと思います。
本書では、この点に絞って説明していきます。
これはゴール付近のことを考えると理解しやすくなります。
ゴール地点にスポットを当てます。
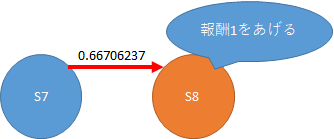
初期状態では上記のとおりQ値は0.66706237と大きいのか小さいのかよくわからない数字ですが、ゴールすると報酬が1もらえます。
ゴール時のQ値は上記と違い、赤枠の部分を0として計算します。そして、S0→S3と異なり、緑枠が1になります。これは大きな報酬です。
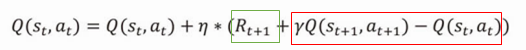
そして、何度も試行してQ値が更新されていくと、最終的にS7→S8のQ値は0.99999…と限りなく1に近づいていきます。
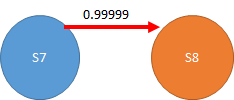
この状態でS4からS7に移動することを考えます。
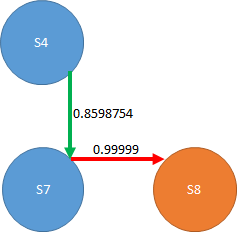
S4からS7に移動するときの計算式は以下となります。
0.8598754 + η*(0 + γ(0.99999 -0.8598754))
TD誤差が小さくなり、緑色の線は0.8598754よりも大きな値に変更されます。
つまり、正解の経路であれば、該当するノードは少しずつ、ゴール手前の経路から順に1に近づいていきます。
一方、ダメ経路を通った場合、例えばS4からS3に戻った場合を見てみます。
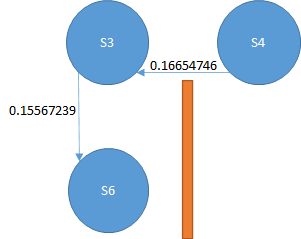
このときのS4から左に移動するときのQ値は以下の式になります。
0.16654746 + η*(0 + γ(0.15567239 -0.16654746))
これはTD誤差がマイナスの値になるので、Q値は0.16654746よりも小さな値になります。
S4が次のノードS3を選ぶ場合、0.16654746程度の価値があるとエージェントは思っています。
この経路に本当に価値があるなら、S4よりもゴールに近いはず(本当は遠いけど)の経路の値はもっと大きな値になっているはずです。
何故なら、ゴールした経路であれば報酬1を得ているからです。つまり、正しい経路ならば、未来に取りうる経路の値はもっと大きいはずです。
ところが、実際には0.16654746よりも価値の低い経路、0.15567239なのでTD誤差はマイナスになります。
そして、S4の経路からS3の経路の価値は低く更新されます。
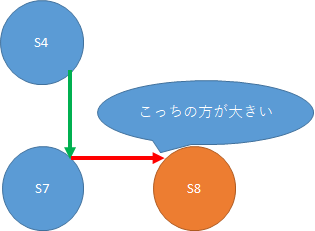
ここが肝です。
学習が進むにつれて、正しい経路ならば、赤のQ値は緑のQ値より大きい、という状態に近づいていきます。
つまり、最終的には以下のようになり、ゴールに最も近いS7→S8間の値はほぼほぼ1になります。
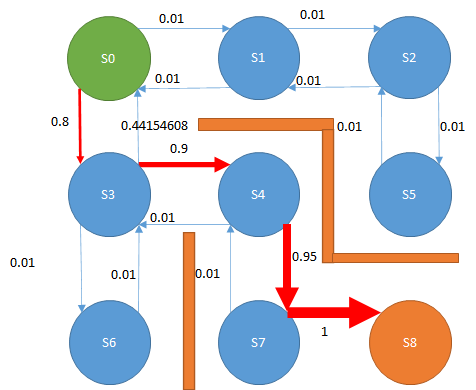
S7→S8が1になると、S4→S7もS7→S8のQ値が大きいのでだんだん1に近づいてきます。
そして、次にS3→S4もS4→S7のQ値が高いので1に近づきやすくなります。
そしてS3→S4も1に近づいてくると、S0→S3も1に近づいてくる、という流れです。
つまり、ゴールのほうからQ値は大きくなっていくということになります。
後は、本を見て学習してください。
Page 2 of 4.
[添付ファイル]
お問い合わせ

すぺぺぺ
自己紹介
本サイトの作成者。
プログラムは趣味と勉強を兼ねて、のんびり本サイトを作っています。
フレームワークはdjango。
ChatGPTで自動プログラム作成に取り組み中。
サイト/ブログ
https://www.osumoi-stdio.com/novel/
