1270 views
はじめに
ゲームストリートファイターVをやっていたのですが、毎日毎日ボコボコにされるのに腹が立ってきて、どうにかやり返せないかと考えたのがきっかけ。
仕事の自動化ならぬ、遊びの自動化を目指します。
となると、必要になるのは強化学習のノウハウ。
そんなわけで、強化学習の勉強を始めました。
基本的にこちらの本をベースに勉強しています。
非常に良い本なのですが、それでもやっぱり強化学習は難しくて、理解出来たつもりでも時間が経つと忘れてしまいそう。
自分の理解を深めるためにアウトプットしていこうと思います。
お題
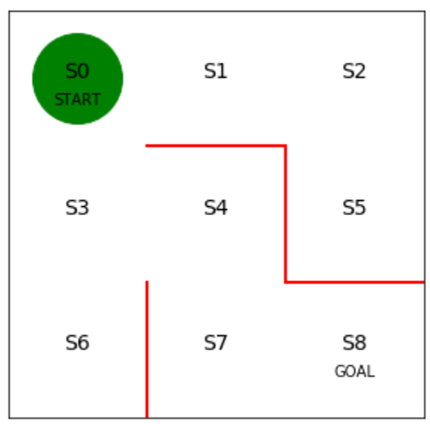
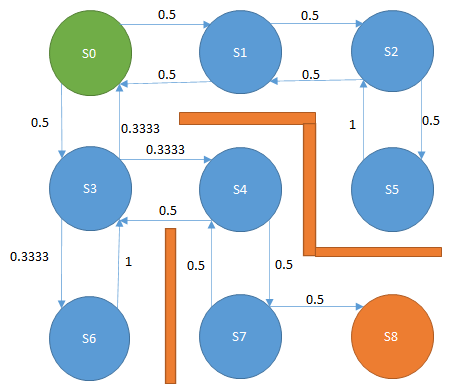
下図の迷路があり、緑色がプレイヤー、赤線は壁、S0~S8はプレイヤーの移動先である。
スタートであるS0からゴールのS8に移動したい。
プレイヤーは上下左右に移動できるが、斜め方向には移動できない。
最短経路である、S0→S3→S4->S7→S8に移動する経路をプログラムで発見するにはどうすればよいか。
手法
方策勾配法を用います。
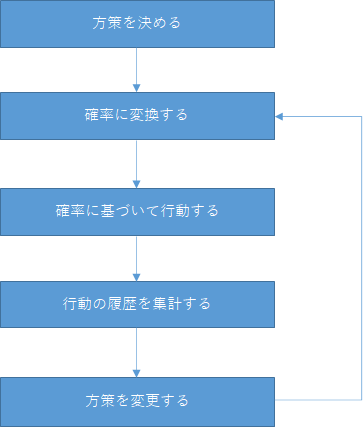
方策勾配法は、ざっくり以下の流れで考えていきます。
- 方策を決める
- 方策を確率に変換する
- 確率に基づいてエージェントを行動させる
- 3.の実行履歴を集計する
- 方策を変更して2.に戻る
方策を決める
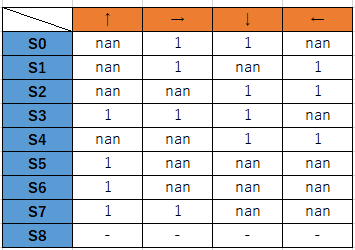
方策というとややこしい感じがしますが、方策ではエージェントが状態ごとに取りうる行動を決めます。
以下が方策のテーブル。左が状態、上が行動を表します。
移動できる場合は1、移動できない場合はnanとします。
S0の行の場合、状態S0において、右と下にだけ移動できる、ということを表しています。
状態遷移図、そういう風に見ても問題ありません。
なお、S8はゴールなので方策はありません。
確率に変換する
上記の方策テーブルを確率に置き換えます。
確率の置き換えはsoftmaxを使います。
softmaxについて詳しく知りたい方は冒頭に紹介した本を参照してください。
とりあえず、各状態において合計が1となるように値を振り分けるイメージです。
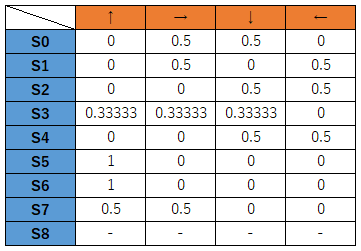
状態S0では、右、または下に移動する確率が0.5、つまり2分の1、上と左には移動しないということを表しています。
図で表すと以下です。
確率に基づいて行動する
確率が決めれたら、エージェントを確率に従って試行させてみます。
つまり、エージェントは最初S0にいるので、右、または下のどちらかに0.5の確率で移動します。
そして、S0の状態で下を選んだ場合、エージェントはS3に移動します。
S3に移動したら、次はS3で取りうる行動をまた確率で決めます。
S3では3分の1の確率で上、右、下のどれか一つを選びます。
これをS8に移動するまで繰り返します。
現時点では、移動できる方向の確率はすべて均等なので、中々ゴールしません。
S8に移動したら、いったん試行を止めます。
注意点として、試行するたびに履歴を残しておく必要があります。
つまり状態S0のときに下を選んだ、S3のときに右を選んだという履歴です。
この履歴を使って、方策、ひいては確率を変更します。
実際に確率に従って行動させたときのデータとしては次のような形式になります。
場所 行動
S0 1
S1 1
S2 2
S5 0
S2 3
S1 1
S2 3
S1 3
S0 1
S1 1
S2 3
S1 3
S0 1
S1 3
S0 2
S3 0
S0 2
S3 2
S6 0
S3 0
S0 1
S1 3
S0 1
S1 3
S0 1
S1 3
S0 2
S3 2
S6 0
S3 2
S6 0
S3 0
S0 2
S3 0
S0 2
S3 1
S4 3
S3 2
S6 0
S3 2
S6 0
S3 2
S6 0
S3 0
S0 2
S3 2
S6 0
S3 0
S0 1
S1 3
S0 1
S1 1
S2 2
S5 0
S2 3
S1 1
S2 3
S1 1
S2 3
S1 1
S2 3
S1 3
S0 2
S3 2
S6 0
S3 0
S0 1
S1 3
S0 2
S3 2
S6 0
S3 1
S4 3
S3 2
S6 0
S3 1
S4 3
S3 2
S6 0
S3 2
S6 0
S3 2
S6 0
S3 0
S0 1
S1 3
S0 1
S1 3
S0 2
S3 2
S6 0
S3 0
S0 2
S3 1
S4 2
S7 0
S4 2
S7 0
S4 2
S7 1
S8 nan
右がエージェントのいる場所、左がその場所でとったエージェントの行動です。
行動の数字の意味は以下です。
- 0:上に移動した
- 1:右に移動した
- 2:下に移動した
- 3:左に移動した
行動の履歴を集計する
上記の履歴テーブルから、次の内容を集計します。
N_ij
各状態で選択した行動の合計値。
例えば、S0で1を選択した回数は履歴中に11回、S0で2を選択した回数は10回あります。
N_i
各状態にいた回数。
履歴テーブルから、S0の場合は21回いたことになります。
T
履歴のレコード数です。102回あります。
方策を変更する
以下の式に当てはめて、方策の値を変更します。
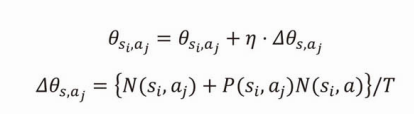
ここが自分には難解だった…。
この計算に、行動の履歴を集計するで集計した値を使います。
方策とは、上述したテーブルのことです。以下に再掲します。

これをtheta[i][j]の2次元配列として考えます。iは0~8の範囲を取り、S0~S8の状態を表します。
jは0~4の範囲を取り、行動を表します。
まずは以下の式です。
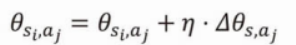
これはプログラム的にはtheta[i][j]の値に小さな値を加算して変更するという意味です。
次に、小さな値の計算方法です。
これが二つ目の式になります。
ちなみに小さな値の式にある、ηという記号がありますが、これはイータと読みます。
0.1など小さな値が入ります。基本的に固定値です。
この小さな値の変数をdelta_theta[i][j]とすると、次の計算になります。
delta_theta[i, j] = (N_ij + pi[i, j] * N_i)/T
です。
pi[i,j]は方策を確率に変換したテーブルのことです。
つまり、以下の表を2次元配列にしたものです。

上記で小さな値が求まったら、その値をtheta[i, j]に加算します。
new_theta[i, j] = theta[i,j] + eta * delta_theta[i, j]
これで方策のテーブルが変更されました。
この方策を使って、エージェントが再試行すると、行動が変わります。
これを100回くらい繰り返すと、最短経路が見つかる、というものです。
何故、この式でゴールに近づいてくのかは謎ですが、詳しくは方策勾配定理を調べてくれとのこと。
だけど、なんかわかりそうでもあります。
一つ目の式、現状の方策に対して小さな値を加算して変更する、というのは機械学習的なノリで理解できます。
問題はその次の小さな値を求める式。
これが理解しづらい。
ここから下はだいぶ間違ってました。近日修正します。
Tの値が大きな意味を持っていた。
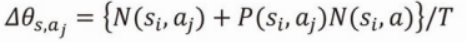
まず、理解しにくい原因ですが、機械学習のパラメーターの値の更新の大前提として、ゴールに関係のある状態と行動に対しては大きな値を加算したい、
ゴールに関係のない値は、加算したくない、という前提があると思っていると思います。
でも、どうやらそうではないようです。
この式は以下のように見えます。
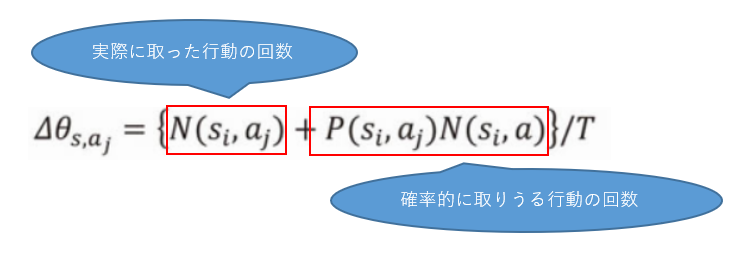
実際に取った行動の回数
N_ijをあてはめます。S0で1を選んだ回数なので11回が入ります。
確率的に取りうる行動の回数
Niに、確率を掛け算します。つまり、NiはS0にいた回数で、Pは1を選ぶ割合を掛け算しています。
つまり、S0において1を選ぶ場合、0.5×21回になり、確率的に1を選ぶはずの回数を計算しています。
基本的に、S0において1を選ぶことに価値があるのかないのか(ないのですが)を考えるときに、実際に取った行動の回数をレコード数で割れば良さそうに思います。
試行回数が増えればゴールに関係のある値だけが加算されていくので、確率的に取りうる行動の回数まで足さなくてもよさそうです。
実際に足さない場合を考えてみます。
試行回数が収束までの中盤あたりになってくると、関係のない経路はほとんど通らなくなってきます。
すると、通らない状態の行動は常に更新が0になってしまいます。
つまり、こんなテーブルになってしまうと、他の行動が全く取れなくなる、ということです。
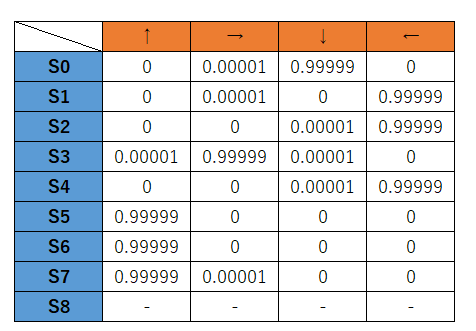
今回の迷路は簡単だからなくてもよいかもしれませんが、複雑な迷路になってくると、ダメだと思っていた経路に活路があるかもしれません。
理想形は以下のような感じで、あまり関係のない経路でも稀に確率的に選ばれるようにして色んな経路を探索できるようにしたい、という意味なのかなぁという解釈です。
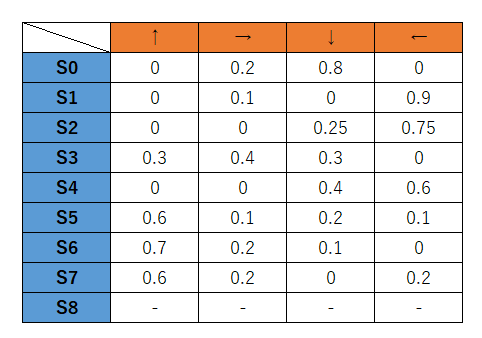
そのため、実際には通らなくてもパラメーターに関しては少しずつ加算しておき、極端な差が出ないようにしているのではないか?という考察です。
Page 1 of 4.
[添付ファイル]
お問い合わせ

すぺぺぺ
自己紹介
本サイトの作成者。
プログラムは趣味と勉強を兼ねて、のんびり本サイトを作っています。
フレームワークはdjango。
ChatGPTで自動プログラム作成に取り組み中。
サイト/ブログ
https://www.osumoi-stdio.com/novel/
