ナップサック問題

Tweet

ナップサック問題、20年くらい前に大学でやったような気がするけど当時はちんぷんかんぷんでした。
ところが最近、仕事でナップサック問題のような内容のプログラムを書く場面があったので改めて復習することにしました。
題材は以下です。
https://atcoder.jp/contests/dp/tasks/dp_d

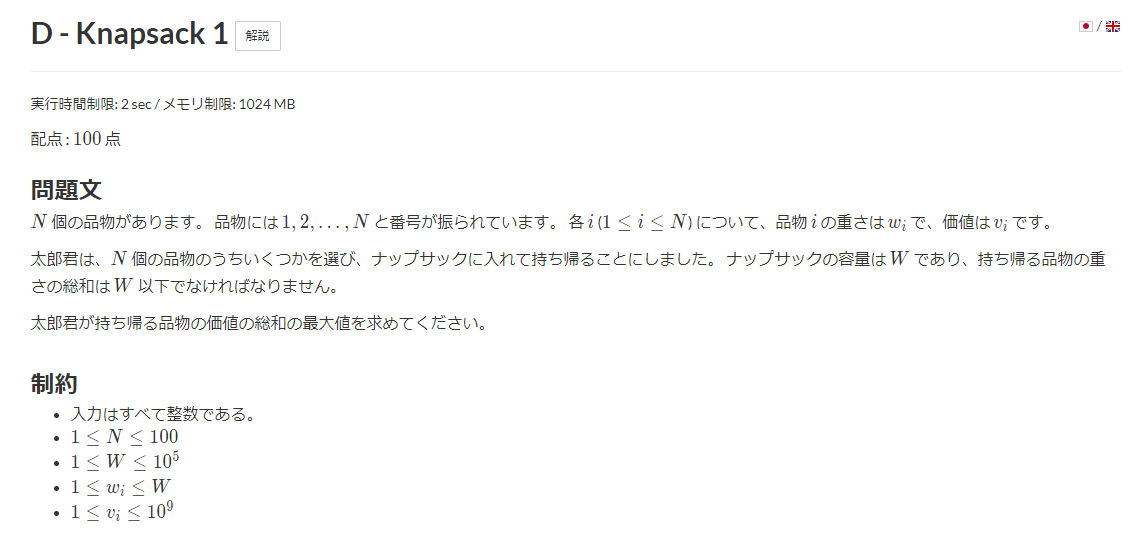
何はともあれ総当たり

問題を簡単にするため、ナップサックに入る重さは8、ナップサックに入れる物の重さと価値は以下とします。

    #(重さ, 価値)のリスト
    data = [(3, 30),
            (4, 50),
            (5, 60)]

動的計画法で解くのがセオリーですが、なぜ動的計画法がセオリーなのかを知るために全探索の問題を記します。
以下が全探索のコード。

# coding:UTF-8

if __name__ == '__main__':
    W = 8 # ナップサックに入る最大の重さ
    #(重さ, 価値)のリスト
    data = [(3, 30),
            (4, 50),
            (5, 60)]

    # 全部の組み合わせを考える
    # それぞれ選ぶかどうかであるから、
    # Trueを鞄に入れる、Falseをカバンに入れないとすると
    patterns = [
        [False, False, False],
        [False, False, True],
        [False, True, False],
        [False, True, True],
        [True, False, False],
        [True, False, True],
        [True, True, False],
        [True, True, True],
    ]

    results = []
    for pattern in patterns:
        total_w = 0
        total_v = 0
        for i, bin in enumerate(pattern):
            if bin:
                # 重さ
                w = data[i][0]
                # 価値
                v = data[i][1]
                total_w += w
                total_v += v

        results.append((total_w, total_v))

    # 重さがW以下で、価値が大きいものを調べる
    max_v = 0
    for result in results:
        w = result[0]
        v = result[1]

        if w <= W:
            if max_v < v:
                max_v = v

    print(max_v)

この解き方で致命傷となるのが処理性能です。
13行目から21行目のパターンの生成ですが、それぞれのモノをナップサックに入れる場合はTrue、入れない場合はFalseとした場合、モノが3個あるので2の3乗で8パターン存在します。
今回は3個なので8パターンですが、ナップサックに入れる物の数が100個等の大きな数字になると、2の100乗のパターンになります。
２の100乗を計算すると、1,267,650,600,228,229,401,496,703,205,376となり、単位が分からんレベルのでかい数になります。
これはコンピューターと言えども生きている間に終わる計算量ではないです。

これを効率的に速くするのが動的計画法。

上の問題を動的計画法で解くと以下。
わかりやすくするために、パターンの計算は手打ち。

# coding:UTF-8

if __name__ == '__main__':
    W = 8 # ナップサックに入る最大の重さ
    #(重さ, 価値)のリスト
    data = [(3, 30),
            (4, 50),
            (5, 60)]

    # 全部の組み合わせを考える
    # それぞれ選ぶかどうかであるから、
    # 1を鞄に入れる、0をカバンに入れないとすると
    patterns = [
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 30, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 30, 50, 0, 0, 80, 0, 0, 0, 0],
        [0, 0, 0, 30, 50, 60, 0, 80, 90, 110, 0, 0],
    ]

    # 重さがW以下で、価値が大きいものを調べる
    max_v = 0
    for pattern in patterns:
        for w, v in enumerate(pattern):
            if w <= W:
                if max_v < v:
                    max_v = v

    print(max_v)

パターンの組み合わせってどう考えるんだ？については
https://www.itmedia.co.jp/enterprise/articles/1005/15/news002.html
が分かりやすい。
patterns変数の
1行目は何も選択しない、
2行目は重さ3のモノを選んだ場合、
3行目は重さ4のモノを選択した場合のパターン、
4行目は重さ5のモノを選択したパターン。

これらの中で最大の価値になるものを探せばよいのだが、ここがやっぱり理解しづらい。
ここの解説について詳しく書きたいな、と思ったけど子供の勉強を見ることになったので続きは明日。