ITパスポート 23年秋 24問 ミニマックス法

Tweet

ITパスポートの23年秋 問24の問題。
これは、ミニマックス法といわれるアルゴリズムを知っていないと解きにくい。

ミニマックス法

将棋のAIなどに使われるアルゴリズム。ゲーム論にカテゴライズされる。
先手、後手で交互に動かすコマを選択する際、先手は自分が有利になるように手を考える。
後手は、先手を邪魔するように手を選ぶ、というのが基本的な考え方。

問題

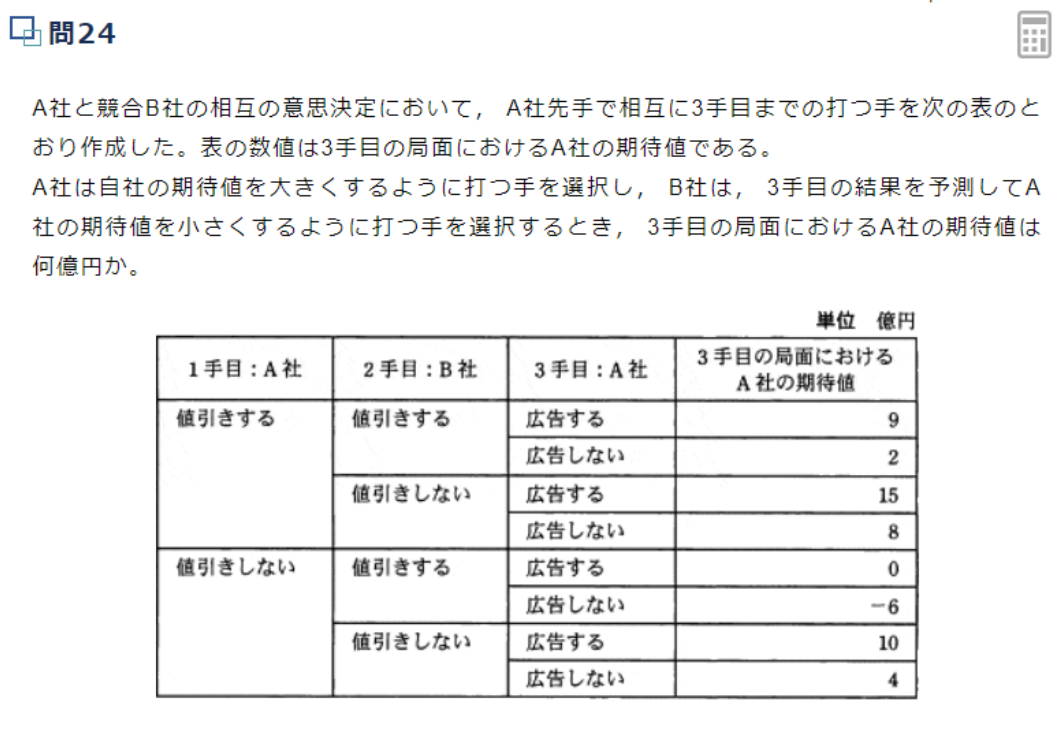
解説

ネタとしては面白い問題だけど、ちょっと例が悪い気もする。
ゲームの得点とかにしたほうが分かりやすいと思う。
問題を言い換えると、以下の前提がある。

• A社は稼ぎたい（得点を稼ぎたい）
• B社はA社の邪魔をしたい（Aの得点を減らしたい）

つまり、先手のA社が何か手を打つと、後手のB社はA社の邪魔になるように行動する、というゲームだ、と考えると理解しやすいと思う。

この前提で、表を見る。
まず、先手のA社は、値引きをするか、値引きをしないかが選べる。

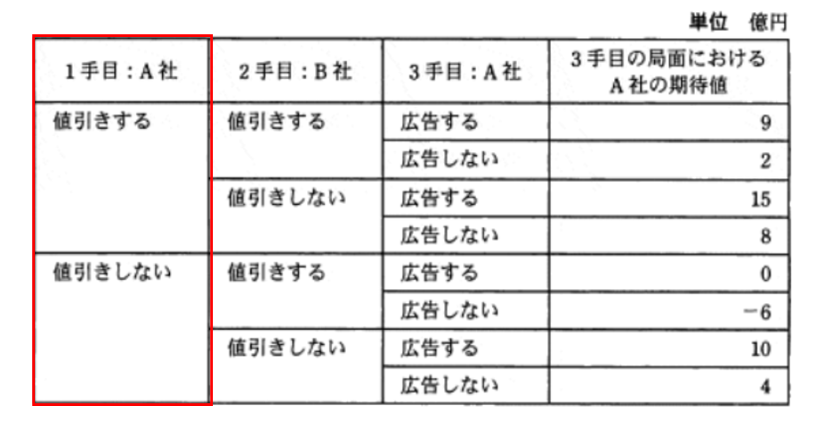
1手目のA社の期待値は「値引きをする」と「値引きをしない」のどちらの期待値が高いと言えるだろうか？
3手目を見据えると、一番稼げるのは15億円の可能性がある、「値引きをする」が正しそうに思える。
つまり、1手目「値引きする」、2手目「値引きしない」、3手目「広告をする」が選べれば15億円が手に入る(下図)。

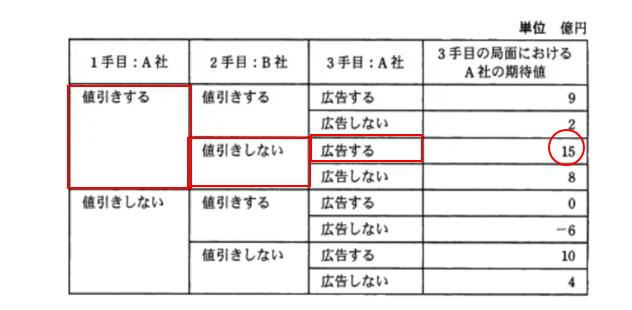
しかし、2手目でB社が「値引きをする」を選ぶとしたら、9億か2億しか稼げない。

一方、1手目でA社が「値引きをしない」を選んだ場合、最悪-6億円にもなってしまうが、奇跡的にすり抜けて、
1手目「値引きしない」2手目「値引きしない」3手目「広告をする」を選ぶと10億円稼げる可能性もある(下図)。

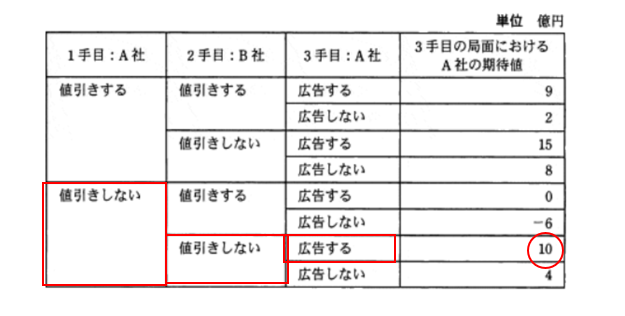
つまり、2手目のB社がどう動くかを予測しないと、1手目の「値引きする」または「値引きしない」のどちらの期待値が高いかはわからない。

次にB社の動きを考える。
例えば、A社は15億円を目指して、1手目を「値引きする」を選んだとする。
すると、B社は、A社の期待値を下げたいので、2手目は絶対に「値引きする」を選ぶ(下図)。

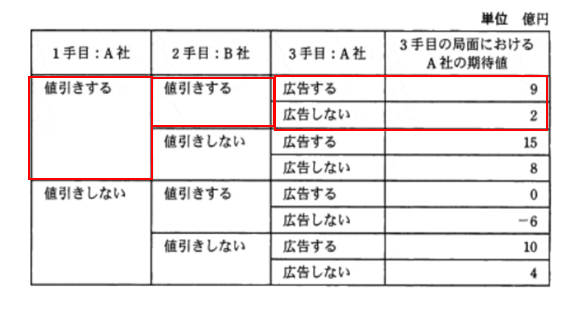
何故なら、2手目でB社が「値引きしない」を選ぶと、3手目でA社は15億円か8億円を選ぶことになるが、そのような状況になれば、A社は絶対に15億円をえらぶことはわかりきっている。それを防ごうと思えば、B社は「値引きする」という選択肢を必然的に選ぶことになる。

…ということをすべてのパターンで考えていけば、解けないこともないのだが、これをもっと機械的に解く方法がある。
それがミニマックス法である。
平たく言えば、逆算みたいなものである。

まず、3手目に至るすべてのパターンにおいて、利益がわかっている。
1手目、2手目で何を選ぶ変わらないが、3手目の各パターンにおいて、A社は、必ず金額の大きいほうを選ぶ(下図)。
つまり、3手目において、「広告する」「広告しない」の期待値が確定する(下図)。

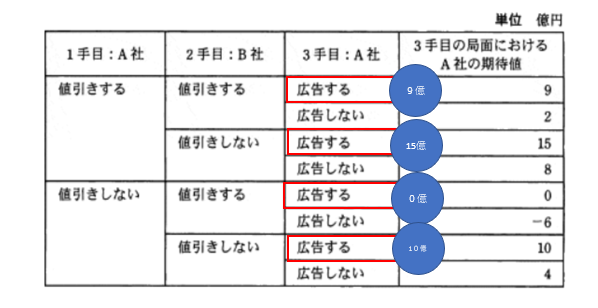
すると、2手目のB社は、A社を9億か、15億か、0億か、10億に誘導できる、と考えられる。
つまり、2手目のB社の期待値は下図のとおりとなり、B社は必ずオレンジ色を選択するといえる。

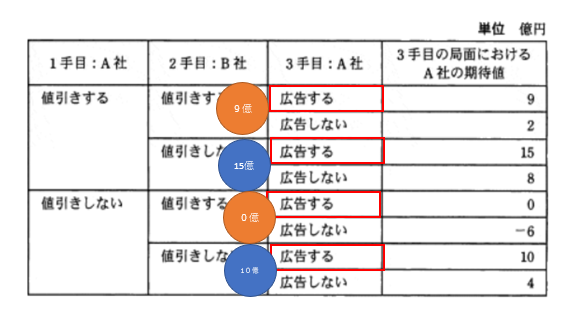
となると、1手目のA社は、「値引きをする」を選んだ時点で9億円コースに誘導され、「値引きをしない」を選ぶと「0億円」コースに誘導される。
つまり、1手目のA社の「値引きをする」の期待値は9億円、「値引きをしない」の期待値は0億円といえる(下図。

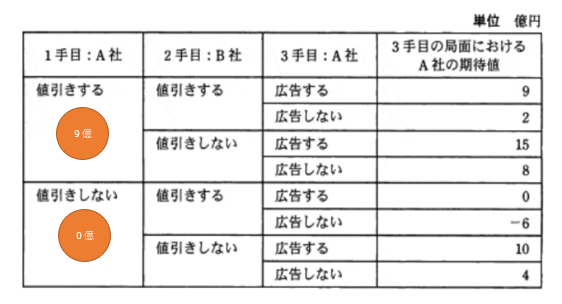
つまり、A社は1手目の期待値は「値引きする」の期待値の方が大きいので、「値引きをする」を選ぶのが正しい。

これをゲーム木で表すと次のようになる。
まず、初期状態は3手目の期待値が分かっている。

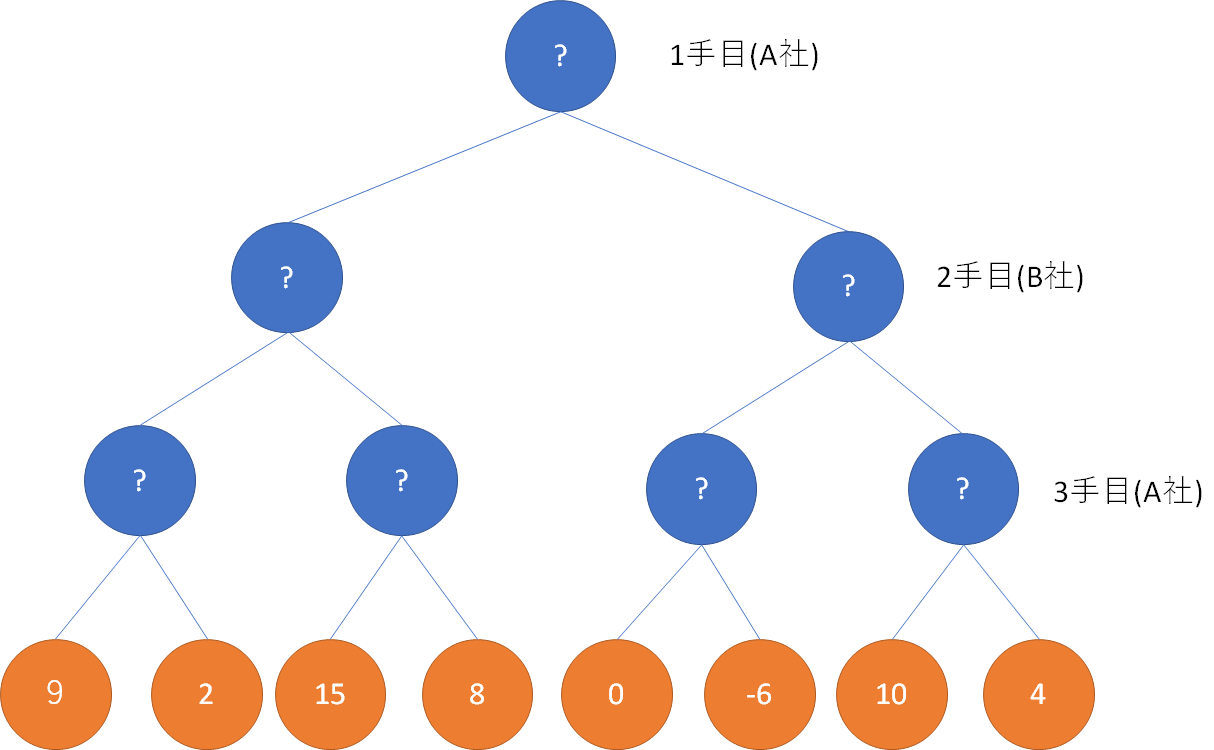
3手目のA社は期待値が大きくなる選択肢を選ぶので、3手目の期待値は次の通りとなる。

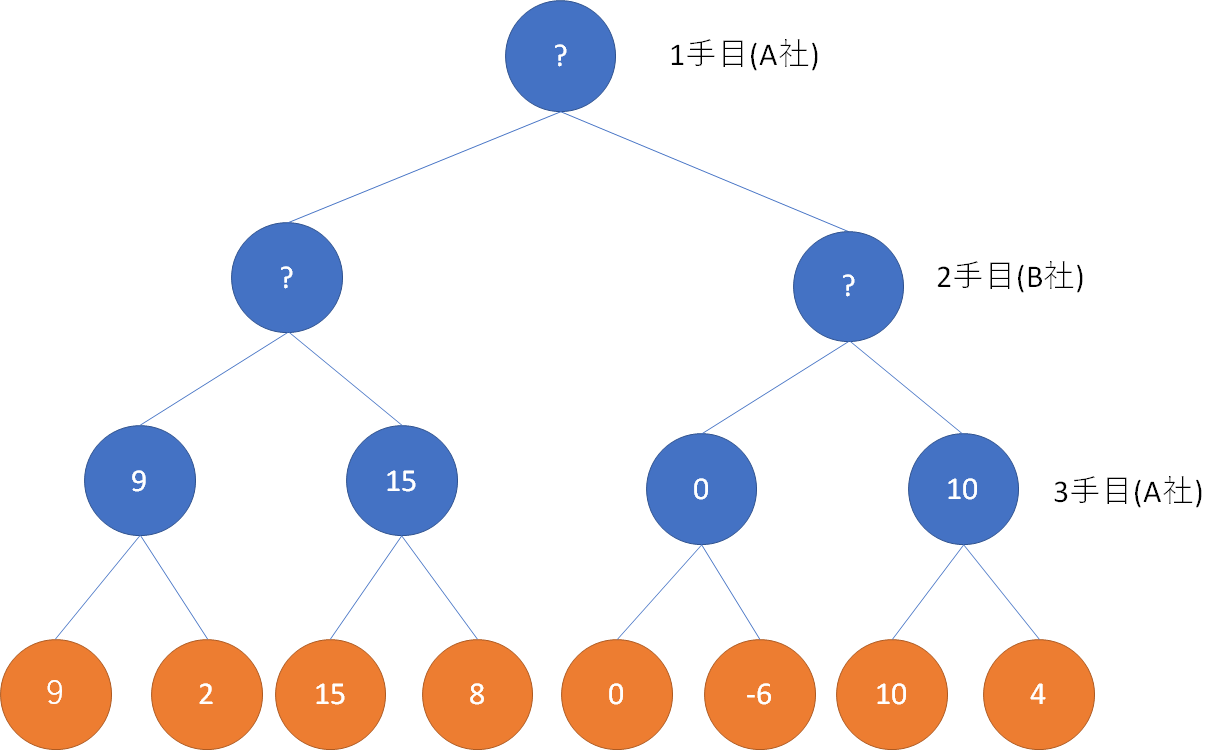
2手目のB社は、それぞれの選択肢において、3手目のA社が得点しにくいほうに誘導するので、2手目の期待値は次の通りとなる。

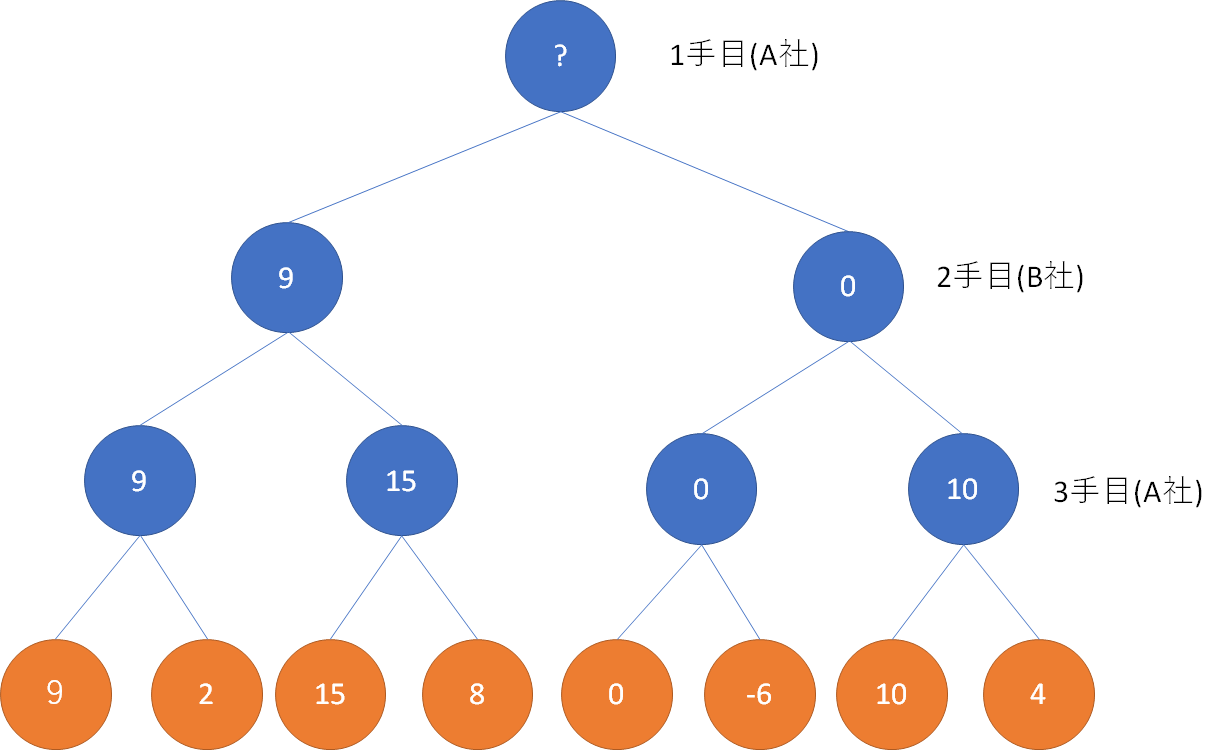
すると、A社は、1手目の時点で9億、または0億が期待値となる。よって、9億を選ぶ。

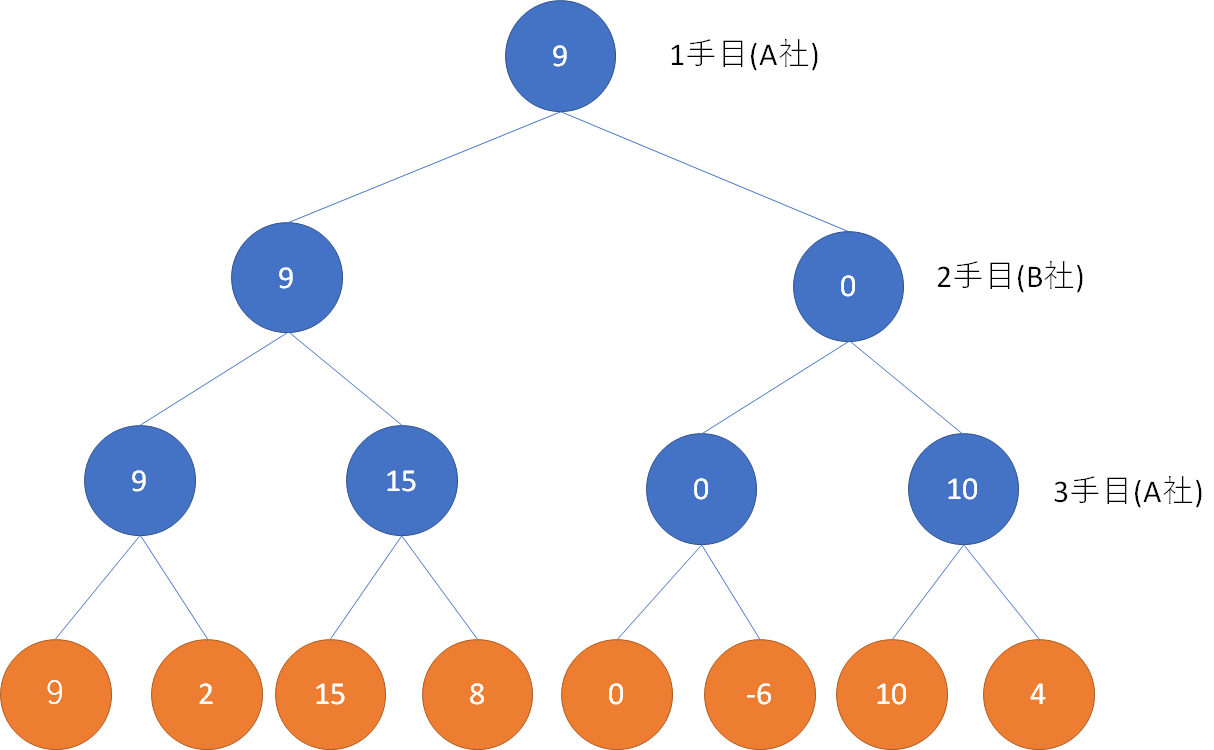
おしまい。