5057 views

そもそも、総当たりってナニ？

まずは、安心と安定の総当たりからやっていきます。
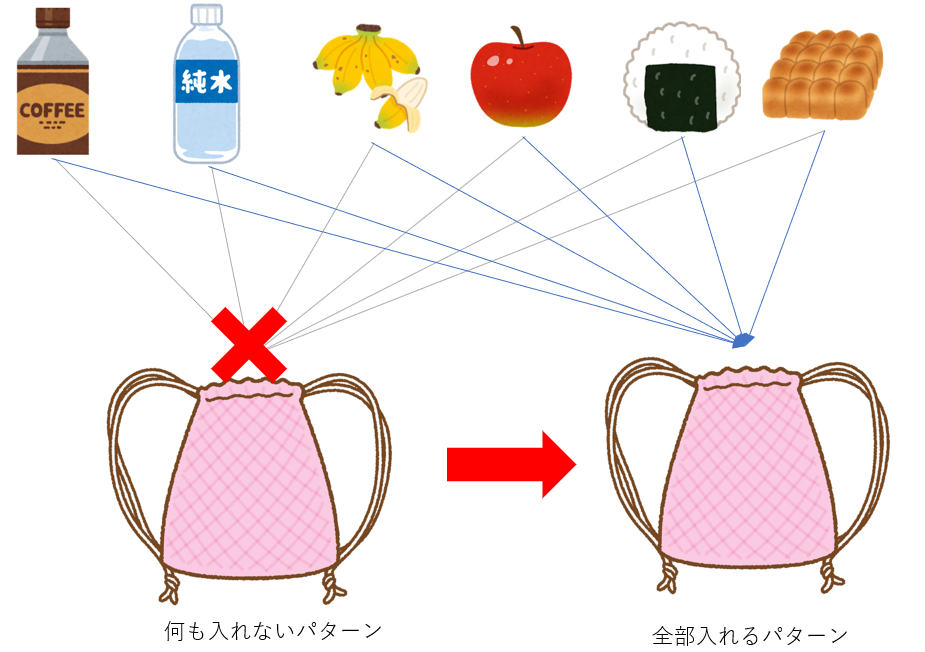
総当たりとは、すべてのパターンを計算することである。
下図のように、ナップサックに何も入れないパターンから、すべて入れるパターンまで、全パターン計算する。

コード

参考：http://zeronosu77108.hatenablog.com/entry/2017/12/25/131726

# 物の個数
n = 6
# 要領
capacity = 65

#物の重さ、価値
size = [10, 12, 7, 9, 21, 16]
price = [120, 130, 80, 100, 250, 185]

#最高の重さと価格と最適な組み合わせを記録する
max_size = -1
max_price = -1
combination = []

# iには2**nまでの値が入る。今回の場合は0～64通り
for i in range(2 ** n):
    # 変数の初期化
    tmp_size = 0
    tmp_price = 0
    tmp_combination = []
    over_flag = False

    for j in range(n):
        # 2進数で計算。シフトして１ビットずつ判断。
        is_put = i >> (n - j - 1) & 1

        # 値を入力
        tmp_combination.append(is_put)
        tmp_size += is_put * size[j]
        tmp_price += is_put * price[j]

        #print(tmp_combination)
        # capa を越えたらフラグを立てて break
        if tmp_size > capacity:
            over_flag = True
            break

    # over flag が立ってない かつ 暫定 max price より高いときに更新
    if (not over_flag) and tmp_price > max_price:
        max_price = tmp_price
        max_size = tmp_size
        combination = tmp_combination

print("合計が最大になる組み合わせ")
print(combination)
print("合計価格: ", max_price)
print("合計サイズ: ", max_size)

出力

これ何やっとる？

少し分けて説明するよ。

変数の話

# 物の個数
n = 6
# 要領
capacity = 65

#物の重さ、価値
size = [10, 12, 7, 9, 21, 16]
price = [120, 130, 80, 100, 250, 185]

#最高の重さと価格と最適な組み合わせを記録する
max_size = -1
max_price = -1
combination = []

今回の例題だと、ナップサックに詰めることができる物は「バナナ」～「コーヒー」までの6つある。
ナップサックの容量は65
sizeとpriceは縦で対応している(size[0]とprice[0]が対応してる)
maxsizeとmaxpricdeには、それぞれ容量と価値
combinationは組み合わせを入れる

処理の流れ

for i in range(2 ** n):
    # 変数の初期化
    tmp_size = 0
    tmp_price = 0
    tmp_combination = []
    over_flag = False

    for j in range(n):
        # 2進数で計算。シフトして１ビットずつ判断。
        is_put = i >> (n - j - 1) & 1

        # 値を入力
        tmp_combination.append(is_put)
        tmp_size += is_put * size[j]
        tmp_price += is_put * price[j]

        #print(tmp_combination)
        # capa を越えたらフラグを立てて break
        if tmp_size > capacity:
            over_flag = True
            break

    # over flag が立ってない かつ 暫定 max price より高いときに更新
    if (not over_flag) and tmp_price > max_price:
        max_price = tmp_price
        max_size = tmp_size
        combination = tmp_combination

この処理では、2進数を使用している。
上のアルゴリズムでは下のような処理をしている。

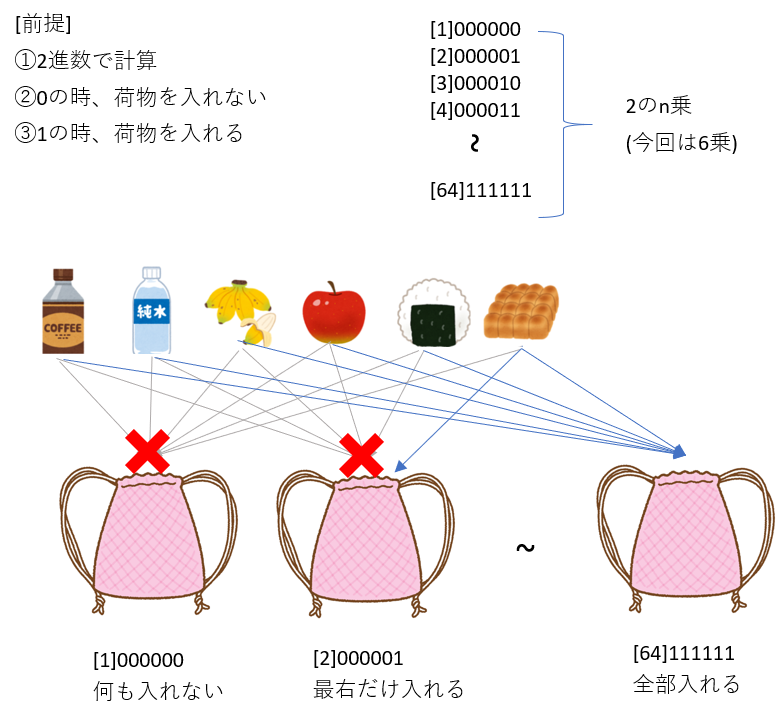
[1]~[64]までの中で、計算して容量に収まりかつ最大の価値を得る組み合わせを計算する。