損失関数と勾配法

Tweet

本章の内容

本章は損失関数の最小値を勾配法で求めると、なぜニューラルが最適化されるのか？という疑問について調べた内容になります。
損失関数と勾配法の基本的な内容はゼロから学ぶDeepLearningでひと通り理解している人向けの記事です。

疑問点

ニューラルネットワークが学習するときのフローを以下の図に記しました。

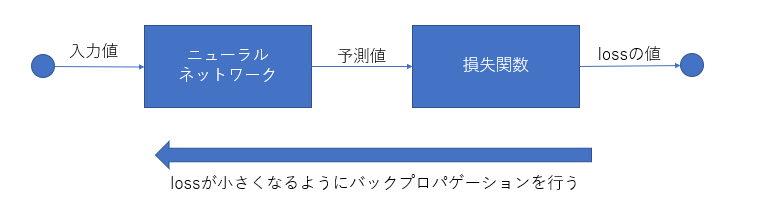
学習するときのフローは、次のとおりです。

[学習時のフロー]
1. 何らかの入力値をニューラルネットワークに渡す
2. 1.の入力に対して、ニューラルネットワークが予測する
3. 予測した値と教師データを比較し、どのくらい乖離しているかを損失関数で求める
4. バックプロパゲーションでニューラルネットワークのパラメーターを更新する

損失関数の値が最小となるパラメーターを見つけるためにバックプロパゲーションを行うわけですが、バックプロパゲーションを行うには、ニューラルネットワークは微分可能な関数である必要があります。

つまり、ニューラルネットワークは何らかの数式なわけです。
しかし、この何らかの数式がはっきりと解説されないため、今一つと理解できない。
何とか可視化して、この疑問を解消したいと思います。

可視化したい

わからないときは、なるべくシンプルな構成で考えてみようということで一番シンプルなパーセプトロンを考えてみました。
以下は一つの入力Xを受けると、一つの出力Yを返すパーセプトロンです。

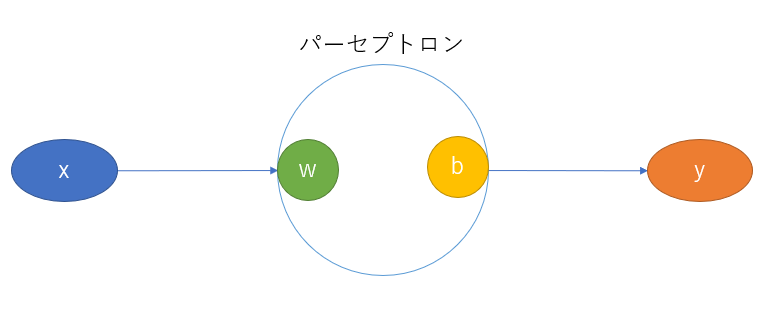
上記のパーセプトロンの計算式は以下となります。

$$
y = wX + b
$$

上記の式はwが傾き、bが切片を表すただの一次関数です。

ここで、例えばパーセプトロンのwが3とbが2だったとします。
そして、教師データはy=2x+1だっだとします。

すると、以下のグラフのようになります。
オレンジ色が教師データ、青色がパーセプトロンが表す直線です。

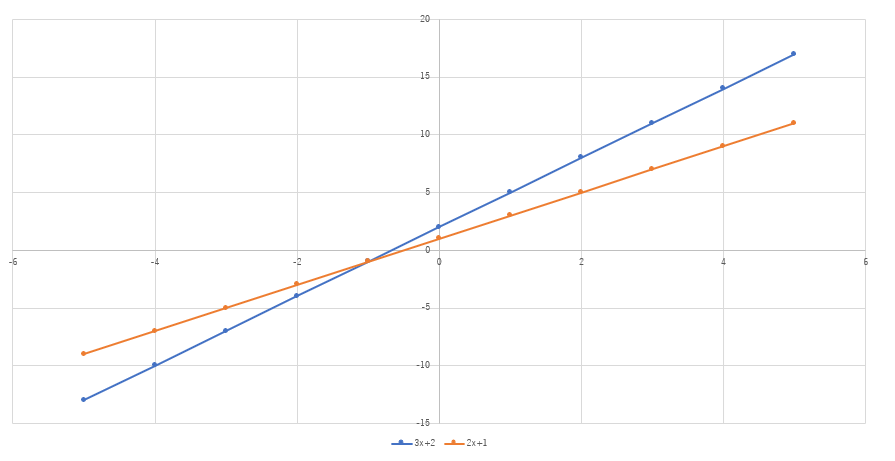
学習によって、パーセプトロンの傾きのwが3から2に、切片のbが2から1に変わると良いわけです。

どうやってwとbを求めているのか

まず、損失関数をMSEとした場合、損失関数の式は次のとおりです。

$$
\text{loss} = \frac{1}{n}\sum_{i=1}^{n}(t - y)^2
$$

yはパーセプトロンが予測した値、tは教師データの値です。
つまり、yは以下の一次関数に置き換えられます。
$$
y = wx + b
$$

損失関数のyとtを実際のパーセプトロンの関数と教師データの関数に置き換えると次のようになります。
$$
\text{loss} = \frac{1}{n}\sum_{i=1}^{n}((3x+2) - (wx+b))^2
$$

そして、wとbを調節してlossが0になるように勾配法で求めることになります。
まず、この数式のグラフを-10≦w≦10、-10≦b≦10の範囲で可視化してみます。
各点は0.5刻みの散布図です。

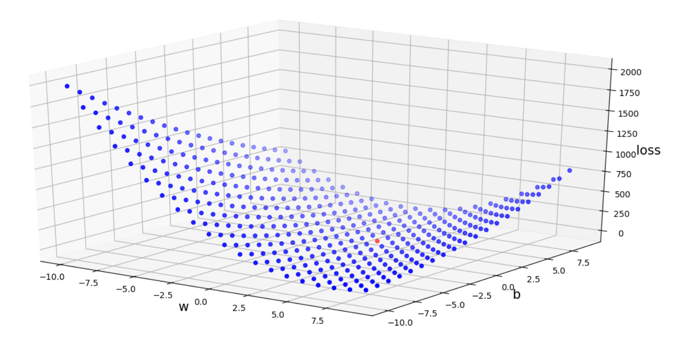
上図の赤い点が最小値(w=2,b=1)のポイントになります。

本当に最小値かわかりにくいので、別の角度から見てみましょう。

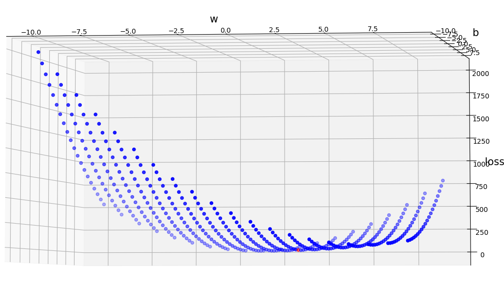
確かに最小値のようです。

損失関数が描くグラフは上図のようになることが分かりました。
バックプロパゲーションでは損失関数を最小に近づけるためにwとbを調節しているのです。

さて、上図の散布図ですが、これは数式でも表せます。
数式で表すと次のようになります。

この式を偏微分を用いて最小値を探していくことになります。

$$
\text{loss} = \frac{1}{n}\sum{i=1}^{n}(yi- (wx_i+b))^2 \
$$

これを展開すると以下になります。
$$
\text{loss} = w^2\sum xi^2 + nb^2 + \sum yi^2 - 2w\sum xiyi - 2b\sum yi + 2wb\sum xi
$$

シグマの部分はすべて定数に変わるので、次の式と考えられます。
シグマを定数のN1～N5で置き換えた式が以下となります。

$$
\text{loss} = w^2N1 + nb^2 + N2 - 2wN3 - 2bN4 + 2wbN_5
$$

この関数はつまるところwとbの2次元の2次関数(何て呼ぶのかわからないので誰か教えてください)です。
後は、勾配法で最小値を探して行けばよいことになります。

ここから先はどうやって最小値を見つけるかですが、その説明に関してはゼロから学ぶDeepLearningに書かれている勾配法の解説の方が分かりやすいので、是非参考にしてみてください。